Apr 02, 2020 The SGP4 model was developed by Ken Cranford in 1970. This model was obtained by simplification of the more extensive analytical theory of Lane and Cranford which uses the solution of Brouwer for its gravitational model and a power density function for its atmospheric model. The SGP4 propagator generates ephemeris in the True Equator Mean Equinox coordinate system based on the epoch of the specified GP data. In addition to certain meta-data, the information contained in the GP data is a set of mean orbital elements that are specific to the SGP4 propagator.

SGP4 is a Simplified General Perturbations mathematical model, which is used to calculate the position of satellites relative to the Earth. The most frequently used model is SGP4, which is used with Two-Line Element (TLE) sets provided by NORAD and NASA.

Sgp49

SGP4 is used for near earth objects with short duration orbital periods (less than 255 minutes). This more than covers all current amateur satellites and the International Space Station. For example, the ISS is about 250 miles above the earth and has an orbital period of about 94 minutes, while FunCube-1 (AO-73) satellite is about 400 miles above the earth and has an orbital period of 97 minutes.

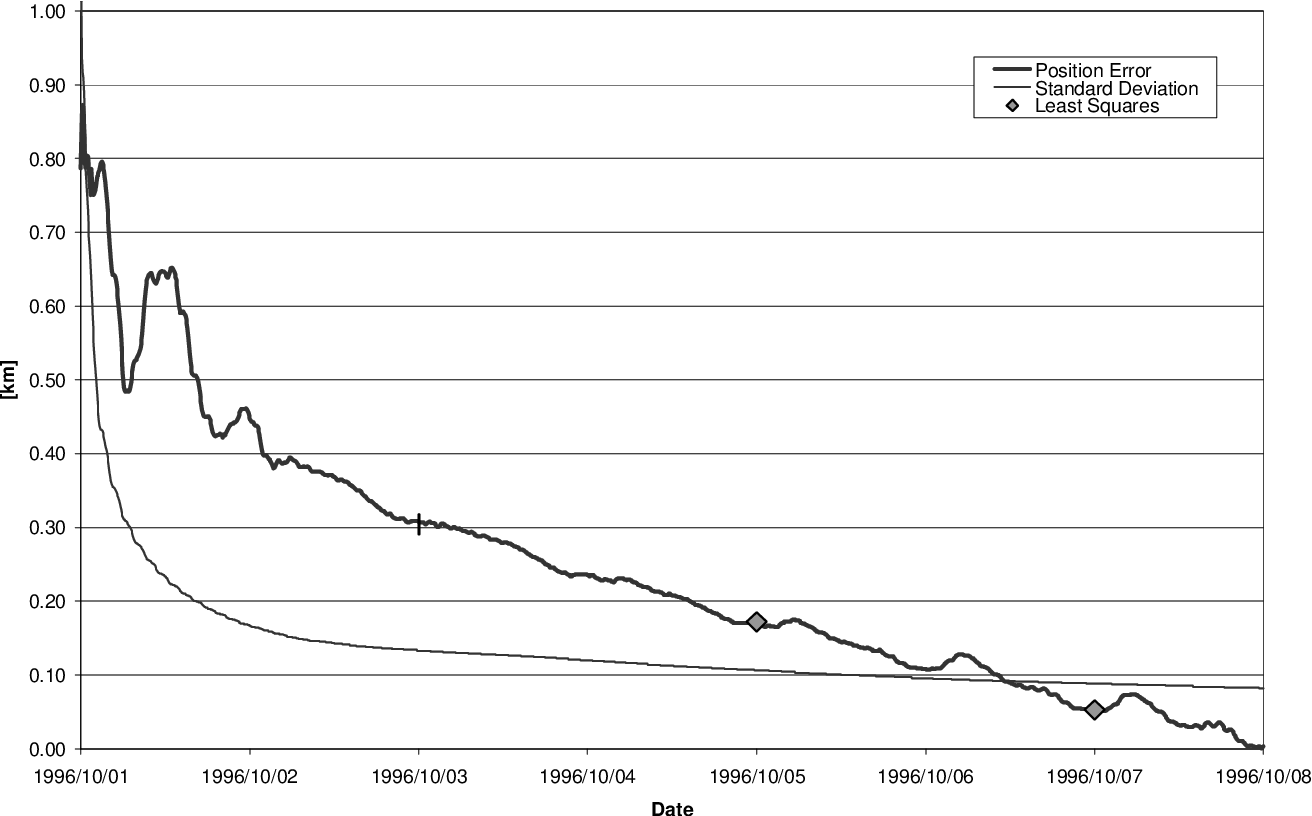
While the original SGP4 calculations were described in Fortran IV back in 1988, they have been ported to many languages, included Python. Due to the critical nature of these prediction models, there are fully automated suites of tests that can be used to validate their accuracy.

A fully tested python version of sgP4 can be found here: https://pypi.python.org/pypi/sgp4/

Sgp4 Equations

Inputs are TLE data and desired time. Output is positional vector and velocity.